- Mathematical Definition: The set of all points such the difference in the distance from two points (called the foci) is a constant. (Kirch)
Algebraically
|
Graphically
|
To classify the equation for a
hyperbola, the standard form needs both terms squared and subtracted like so 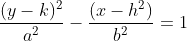 or  . To find the points of the
hyperbola we start with the center. (h,k) is our center. Then we look to find
our ‘a’ value which is the distance from the center to the vertices and can
be determined from the first denominator of the equation square rooted. The
second denominator will be the ‘b’ value determining the distance from the
center to the co-vertices. To find whether the graph is going to open
left/right or up/down, we look to the first squared term. If x is squared
first then the transverse axis will be horizontal meaning that the graph will
go left/right. If y is squared first then the transverse axis will be
vertical meaning that the graph will go up/down. The transverse and conjugate
axis will always cross the center so if the transverse is on the x-value,
then the conjugate is on the y-value, vice versa. To find the vertices, you
can simply count from the center by the ‘a’ value, or add. It’s the same with
the co-vertices with the ‘b’ value. Then there is the ‘c’ value that will
give you the foci. For that we use c^2=a^2+b^2. For actually calculating the
asymptotes in the slope-intercept form, we use  if the graph is going left/right and if the graph is going left/right and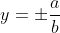 or |
A
hyperbola looks like an ellipse that stretched so wide that it snapped in
half and left it’s two halves going in opposite directions. Basically, the
opposite-directions effect is caused by the foci which instead of being inside
an ellipse are outside. Thus instead of the graph being a set of points for
which the sum of distances from foci is a fixed constant, the difference of distances from the foci
is a fixed constant. (Kirch)
In this case, the constant is 2. Since the
hyperbola is what farthest deviates from a circle, its eccentricity is
greater than 1. Other parts of a hyperbola are the transverse and conjugate
axis, two diagonal asymptotes, the center, vertices, co-vertices, and two
branches. The transverse axis is determined by which term goes first in the
equation or the vertices. The conjugate axis is determined as perpendicular
to the transverse axis and also determined by the co-vertices. When drawing a
rectangle from the transverse and conjugate axis, the two asymptotes go
diagonally straight through it, never ending until it hits the graphs limits.
All this is connected and crossing the center. The branches will be opening
left/right or up/down, never touching the asymptotes and only the vertices.
VIDEO BELOW |
3.
RWA: Hyperbolic structures can be made out of straight beams, much easier than using curved beams that aren't as stable or strong. These structures make up water towers, cooling towers, and aesthetic features. The structure is very useful for radioactive cooling towers where at the bottom, the widening of the tower provides the area for installation of fill to cool circulated water. The narrowing of the middle helps support turbulent mixing when it then rises out of the widened opening.
Many architects used the hyperbolic structure to make famous, looming buildings like the Church of Colonia Guell. Zarzuela, and the Kobe Port Tower. These towers were made my stacking sections of hyperboloids while supporting them with shape defining rings.
4.
REFERENCES/WORKS CITED
https://www.youtube.com/watch?v=Z6cwpsDC_5A
http://www.lessonpaths.com/learn/i/unit-m-conic-section-applets/hyperbola-from-the-definition-geogebra-dynamic-worksheet
http://www.lessonpaths.com/learn/i/unit-m-conic-section-applets/all-the-conic-sections
http://www.pleacher.com/mp/mlessons/calculus/apphyper.html
http://en.wikipedia.org/wiki/Hyperboloid_structure
