GRAPH
cloud radical 9
Sunday, June 1, 2014
Monday, May 19, 2014
BQ #6: Unit U Concept Intro-8: Limits
1.(a) What is continuity?
Continuity is when a graph/function is predictable meaning you can tell where it's going. It is also where there are no breaks, no jumps, and no holes in the graph. A continuous graph can be drawn without lifting your pencil. Lastly, when the graph is approaching an infinite amount of x-values from the right and left, the graph meets at the same f(x), limit, and value meaning the limit equals the value.
(b) What is discontinuity?
Discontinuity is when a graph/function has breaks, jumps, and holes. There are four types of discontinuities separated into two families. The families are named Removable and Non-removable discontinuities whereas Point discontinuity is the only removable discontinuity, and the remaining three non-removable discontinuities are Jump, Infinite, and Oscillating. A Point discontinuity is a graph that contains a hole. There may be a value above or below the hole or it can remain undefined. A Jump discontinuity looks like the graph got cut and slid up/down. The end points of the jump can be open-holed + open-holed (the value is undefined) or open-holed+closed-hole (the value is the close-holed point). The end points cannot be close-holed+close-holed b/c that defies the vertical line test meaning that it's not a function. An Infinite discontinuity is a graph split by asymptote(s). It's usually a vertical asymptote in which leads to unbounded behavior meaning the graph is going to positive/negative infinity. An Oscillating discontinuity is a graph that wiggles similarly to a sin/cos graph but begins to thin towards a point in the graph and then widens again.
2. (a) What is a limit?
A limit is the intended height of a function. A limit is basically where the graph intends or plans to reach a point.
(b) When does a limit exist?
A limit exists when the graph is either continuous or inhibits point discontinuity. This is b/c the graph approaching an x-value from the right & left both meet at the same exact y-value.
(c) When does a limit not exist?
The limit does not exist in three cases. One: the graph approaching an x-value from the right & left do not reach the same y-value. Two: the graph inhibits a vertical asymptote which thus creates unbounded behavior. This means that the limit is +/- infinity which can't happen because +/- infinity isn't a number. Three: the graph exhibits oscillating behavior where the graph doesn't concentrate or approach on a single point (the wiggles are too intense!).
(d) What is the difference between a limit and a value?
A limit is the intended height while a value is the actual height. If the value is undefined at one point, the limit may or may not exist depending on if the graph approaches that point from the left and right. If a limit does not exist, the value may still exist if there is a plotted, closed-hole point that is present above or below the open-hole.
3. How do we evaluate limits numerically, graphically, and algebraically?
Numerically: we need to set up an x|y table to show as x approaches a # (in decimals!) from the left and right (-/+). For example, if we want to approach 2, we'd write {1.9, 1.99, 1.999, 2, 2.001, 2.01, 2.1}. We fill out the y column by punching in the #s on our graphing calculator! Graphically: we take our left index finger and stick it on the left side of the graph, then we take our right index finger and stick it on the right side of the graph and then start moving both fingers toward the ends of the graph. If our fingers meet, the limit exists at that y-value! If they do not meet, then the limit does not exist!!! (wow) Algebraically: There are four methods that come one after another. The first and easiest is direct substitution in which we plug the # x is approaching into the function. You can get four types of answers: a #, 0/# = 0, #/0 = ø, and lastly 0/0 = indeterminate form/not yet determined. If we get 0/0 there are three ways to solve it out: the dividing out/factoring method, the rationalizing/conjugate method, and solving limits at infinity. The dividing out/factoring method applies mostly to polynomials that you can factor out, then cancel something equal to 1, and use direct substitution. If there are no polynomials but instead radicals, we use rationalizing/conjugate method. We take the conjugate of the numerator/denominator WITH the radical (the conjugate is the change of the plus/minus sign to the opposite)and take this so to multiply it to the numerator & denominator giving us something to cancel and again use direct substitution. The last method is used only for limits at infinity confirming the presence of a horizontal asymptote. The easy way to solve these is to remember the use of the degree (exponent). If the degree was Bigger on Bottom, the y value was 0, or if it was the same then it'd be the ratio of the coefficients, and if it was Bigger on Top it'd be undefined and the limit wouldn't exist b/c of unbounded behavior. The long way is by dividing every term in the numerator and denominator by the highest power of x in the denominator and then using direct substitution. (note: #/infinity = 0)
TY FOR READIN' & HAVE A GOOD NIGHT!
Continuity is when a graph/function is predictable meaning you can tell where it's going. It is also where there are no breaks, no jumps, and no holes in the graph. A continuous graph can be drawn without lifting your pencil. Lastly, when the graph is approaching an infinite amount of x-values from the right and left, the graph meets at the same f(x), limit, and value meaning the limit equals the value.
(b) What is discontinuity?
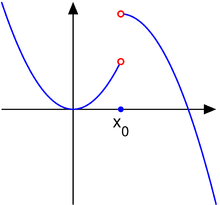 |
| JUMP |
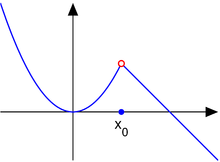 |
| POINT |
 |
| OSCILLATING (left) INFINITE (right) |
2. (a) What is a limit?
A limit is the intended height of a function. A limit is basically where the graph intends or plans to reach a point.
(b) When does a limit exist?
A limit exists when the graph is either continuous or inhibits point discontinuity. This is b/c the graph approaching an x-value from the right & left both meet at the same exact y-value.
(c) When does a limit not exist?
The limit does not exist in three cases. One: the graph approaching an x-value from the right & left do not reach the same y-value. Two: the graph inhibits a vertical asymptote which thus creates unbounded behavior. This means that the limit is +/- infinity which can't happen because +/- infinity isn't a number. Three: the graph exhibits oscillating behavior where the graph doesn't concentrate or approach on a single point (the wiggles are too intense!).
(d) What is the difference between a limit and a value?
A limit is the intended height while a value is the actual height. If the value is undefined at one point, the limit may or may not exist depending on if the graph approaches that point from the left and right. If a limit does not exist, the value may still exist if there is a plotted, closed-hole point that is present above or below the open-hole.
3. How do we evaluate limits numerically, graphically, and algebraically?
Numerically: we need to set up an x|y table to show as x approaches a # (in decimals!) from the left and right (-/+). For example, if we want to approach 2, we'd write {1.9, 1.99, 1.999, 2, 2.001, 2.01, 2.1}. We fill out the y column by punching in the #s on our graphing calculator! Graphically: we take our left index finger and stick it on the left side of the graph, then we take our right index finger and stick it on the right side of the graph and then start moving both fingers toward the ends of the graph. If our fingers meet, the limit exists at that y-value! If they do not meet, then the limit does not exist!!! (wow) Algebraically: There are four methods that come one after another. The first and easiest is direct substitution in which we plug the # x is approaching into the function. You can get four types of answers: a #, 0/# = 0, #/0 = ø, and lastly 0/0 = indeterminate form/not yet determined. If we get 0/0 there are three ways to solve it out: the dividing out/factoring method, the rationalizing/conjugate method, and solving limits at infinity. The dividing out/factoring method applies mostly to polynomials that you can factor out, then cancel something equal to 1, and use direct substitution. If there are no polynomials but instead radicals, we use rationalizing/conjugate method. We take the conjugate of the numerator/denominator WITH the radical (the conjugate is the change of the plus/minus sign to the opposite)and take this so to multiply it to the numerator & denominator giving us something to cancel and again use direct substitution. The last method is used only for limits at infinity confirming the presence of a horizontal asymptote. The easy way to solve these is to remember the use of the degree (exponent). If the degree was Bigger on Bottom, the y value was 0, or if it was the same then it'd be the ratio of the coefficients, and if it was Bigger on Top it'd be undefined and the limit wouldn't exist b/c of unbounded behavior. The long way is by dividing every term in the numerator and denominator by the highest power of x in the denominator and then using direct substitution. (note: #/infinity = 0)
TY FOR READIN' & HAVE A GOOD NIGHT!
Monday, April 21, 2014
BQ #3 Unit T Concepts 1-3
How do the graphs of sine and cosine relate to each of the others? a) Tangent?
Tangent's ratio identity is sin/cos. As cosine equals zero, tan is undefined meaning it will not touch wherever cosine equals zero. As sine equals zero however, tan will intersect the x-axis because tan will equal zero.
b) Cotangent?
Cotangent's ratio identity is cos/sin. As sine equals zero, cot is undefined meaning it will not touch wherever sine equals zero. As cosine equals zero however, cot will intersect the x-axis because cot will equal zero.
c) Secant?
Secant's reciprocal identity is 1/cos. That means whenever cosine equals 0, then secant will be undefined and will never touch wherever cosine equals 0. When cosine equals 1, secant will equal 1 thus the amplitudes of secant and cosine will touch.
d) Cosecant?
Cosecant's reciprocal identity is 1/sin. That means whenever sine equals 0, cosecant will be undefined and will never touch wherever sine equals 0. When sine equals 1, cosecant will equal 1 thus the amplitudes of cosecant and sine will touch.
Sunday, April 20, 2014
B#5 Unit T Concept 1-3
Why do sine and cosine NOT have asymptotes, but the other four trig graphs do?
To have asymptotes your trig function has to be undefined at some point which is when the denominator equals 0.
Sine and Cosine don't have asymptotes because when you take a right triangle from the unit circle starting at (0,0) sine and cosine have the denominator of r which is the radius of the unit circle. The radius is always 1. Since the radius can never be zero, sine and cosine are never undefined.
All other trig functions have asymptotes because their denominators can equal 0 and thus make the trig function undefined. Also with the same variable denominators like tan and csc, they have the same asymptotes!
Saturday, April 19, 2014
BQ#4 Unit T Concept 3
Why is a "normal" tangent graph uphill, but a "normal" tangent graph downhill?
If you take a look at the graph of tangent (top), the asymptotes starting from (0,0) are at pi and 3pi/2. These are also where cosine is zero and touches the x-axis. When remembering trig identities, tan = sin/cos. If Cosine is zero, that means tan is undefined and it's graph cannot exist where cosine is zero which is why the asymptotes are there. It goes uphill because starting from (0,0) the first quadrant it 0 to pi/2 where tan is positive. The graph goes up and along the asymptote positively. After the asymptote, tan is negative II quadrant but positive III quadrant so the graph starts negative up against (but not touching!) the asymptote and then curving up positive against the asymptote making an uphill curve.
For the cot graph (bottom), the asymptotes are shifted! The asymptotes are now at 0 and pi, where sine is 0. The identity states that cot = cos/sin, the reciprocal of tan's identity. Where cosine is zero, cot is undefined and the cot graph cannot touch where cosine is zero. The graph goes downhill because the asymptote starts at (0,0) and quadrant I starts there. Thus the graph will start against the asymptote going down into quadrant II which is negative and staying there because of the next asymptote at pi. This makes the downhill curve.
Friday, April 18, 2014
BQ#2 Unit T: Concept 1
How do Trig Graphs relate to the Unit Circle?
a) Period-Why is the period for sine and cosine 2 pi, whereas the period for tangent and cotangent is pi?

According to the unit circle, sin is positive in quadrants I and II whereas quadrants III and IV are negative making the pattern +, +, -, -. Cos is positive in quadrants I and IV whereas quadrants II and III are negative making the patter +, -, -, +. It takes a whole unit circle to complete a pattern until it repeats itself. When you look at a unit circle, the circumference is 2pi. If you cut it at one point and laid it flat, it would still be a length of 2pi. That is basically a sine and cosine graph's period. You can also see the patterns represented on the graph.
b) Amplitude?-How does the fact that sine and cosine have amplitudes of one (and the other trig functions don't have amplitudes) relate to what we know about the Unit Circle?
This is because in the unit circle they are restricted to (0,1), (-1,0), (1,0), (0,-1) or restricted from -1 to 1 which is the radius of the Unit Circle. This creates walls for the sin/cos graphs and thus they have amplitudes of one.
Wednesday, April 2, 2014
Subscribe to:
Posts (Atom)










